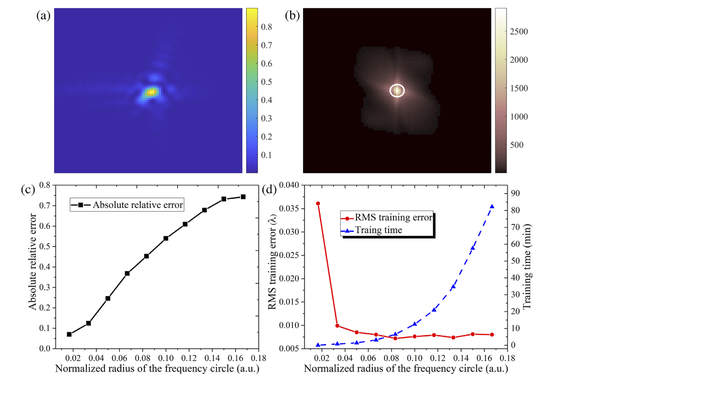
Abstract
Phase diversity wavefront sensing (PDWS) has been a successful approach to quantifying wavefront aberrations with only a few intensity measurements and nonlinear optimization. However, the inherent non-convexity of the inverse problem may lead to stagnation at a local minimum far from the true solution. Proper initialization of the nonlinear optimization is important to avoid local minima and improve wavefront retrieval accuracy. In this paper, we propose an effective neural network based on low-frequency coefficients in the Fourier domain to determine a better estimate of the unknown aberrations. By virtue of the proposed network, only a small amount of simulation data suffice for a robust training, two orders of magnitude less than those in existing work. Experimental results show that, when compared with some existing methods, our method achieves the highest accuracy while drastically reducing the training time to 1.4 min. The minimum, maximum, and mean values of the root mean square (RMS) residual errors for 800 aberrations are 0.017λ, 0.056λ, and 0.039λ, respectively, and 95% of the RMS residual errors are less than 0.05λ.